先在开头总结一下，二叉树解题的思维模式分两类：

1、是否可以通过遍历一遍二叉树得到答案？如果可以，用一个 traverse 函数配合外部变量来实现，这叫「遍历」的思维模式。

2、是否可以定义一个递归函数，通过子问题（子树）的答案推导出原问题的答案？如果可以，写出这个递归函数的定义，并充分利用这个函数的返回值，这叫「分解问题」的思维模式。

无论使用哪种思维模式，你都需要思考：

如果单独抽出一个二叉树节点，它需要做什么事情？需要在什么时候（前/中/后序位置）做？其他的节点不用你操心，递归函数会帮你在所有节点上执行相同的操作。

下文通过几道简单的题目，实践运用这几条总纲，理解「遍历」和「分解问题」的思维又和区别和联系

二叉树相关的题目，无非是在二叉树遍历时的前序/中序/后续位置做文章，当然这并不能包含所有的，但是大部分如此，万变不离其宗，因此我们可以定义出一个基础框架：

1
2
3
4
5
6
7
8
9
10
func traverse(root *TreeNode){
    if root == nil {
        return
    }
    // 前序位置
    traverse(root.Left)
    // 中序位置
    traverse(root.Right)
    // 后序位置
}

先不管所以为的前中后序，单看traverse，他在做的无非就是把整个二叉树所有节点遍历一遍，本质上与你遍历数组和链表类似。

144. 二叉树的前序遍历

image-20220915081346242

解题思路：

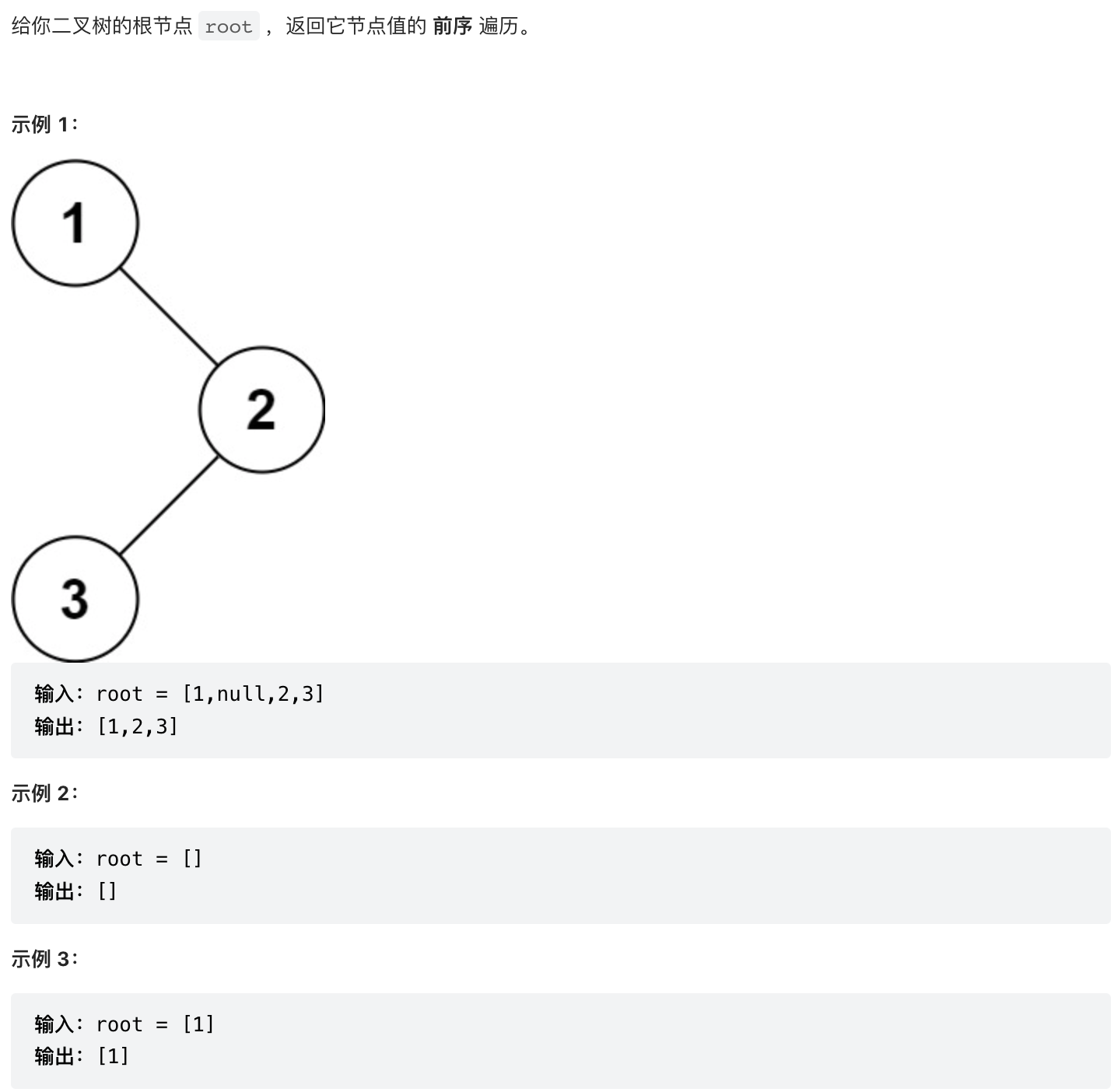
经典二叉树前序遍历，二叉树入门级题目，套入上文的框架，前序遍历则在前序位置将节点放入数组即可

示例代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
var list []int

func preorderTraversal(root *TreeNode) []int {
   preorder(root)
   return list
}

func preorder(node *TreeNode) {
   if node == nil {
      return
   }
   list = append(list, node.Val)
   preorder(node.Left)
   preorder(node.Right)
}

上述代码使用了全局变量，在leetcode提交时会有问题，稍微改造一下即可

1
2
3
4
5
6
7
8
9
10
11
12
13
14
func preorderTraversal(root *TreeNode) []int {
   var list []int
   var preorder func(node *TreeNode)
   preorder = func(node *TreeNode) {
      if node == nil {
         return
      }
      list = append(list, node.Val)
      preorder(node.Left)
      preorder(node.Right)
   }
   preorder(root)
   return list
}

解题思路：

二叉树的前序遍历，是先拿出根节点，再拿到左子树的节点，再拿到右子树的节点，将他们三个合并到一起，就是一颗二叉树的前序遍历。我们把一整颗二叉树的遍历分解成一个又一个小数的遍历，最后合并到一起，这就是分解的思路

示例代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
func preorderTraversal(root *TreeNode) []int {
   var res []int
   if root == nil {
      return res
   }

   // 分解
   left := preorderTraversal(root.Left)
   right := preorderTraversal(root.Right)

   // 合并
   res = append(res, root.Val)
   res = append(res, left...)
   res = append(res, right...)
   return res
}

145. 二叉树的后序遍历

image-20220915224053997

解题思路：

两种思路与上一题都一致，唯一不同时根据顺序调整插入当前节点的位置

示例代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
// 遍历
func postorderTraversal(root *TreeNode) []int {
	var list []int
	var preorder func(node *TreeNode)
	preorder = func(node *TreeNode) {
		if node == nil {
			return
		}
		preorder(node.Left)
		preorder(node.Right)
		list = append(list, node.Val)
	}
	preorder(root)
	return list
}

// 分解
func postorderTraversal2(root *TreeNode) []int {
	var res []int
	if root == nil {
		return res
	}

	// 分解
	left := postorderTraversal2(root.Left)
	right := postorderTraversal2(root.Right)

	// 合并
	res = append(res, left...)
	res = append(res, right...)
	res = append(res, root.Val)
	return res
}

104. 二叉树的最大深度

image-20220915225409195

解题思路：

定义两个全局变量res和depth，res负责记录最大深度，depth像一个游标，跟着递归遍历到每一个节点记录其深度，向下遍历时depth++，返回时depth--

示例代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
unc maxDepth(root *TreeNode) int {
    var traverse func(root *TreeNode)
    var depth int
    var result int
    traverse = func (root *TreeNode) {
	    if root == nil {
		    return
	    }
	    // 前序位置
	    depth++
	    if root.Left == nil && root.Right == nil {
            // 到达叶子节点,更新最大深度
		    if depth > result {
			    result = depth
		    }
	    }
	    traverse(root.Left)
	    traverse(root.Right)
	    // 后序位置
	    depth--
    }
	traverse(root)
	return  result
}

解题思路：

一个二叉树的最大深度可以通过子树的最大深度推倒出来，所以我们只需要求出一个子树的最大深度即可

一个树的最大深度就是左子树或是右子树深度中最大值，在加上自身就是这颗树的最大深度

示例代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
func maxDepth(root *TreeNode) int {
   	if root == nil {
      	return 0
   	}
	// 计算左右子树的最大深度
   	leftMax := maxDepth(root.Left)
   	rightMax := maxDepth(root.Right)
    // 整棵树的最大深度等于左右子树深度的最大值，在加上自己
   	if leftMax < rightMax {
      	return rightMax + 1
   	}
   	return leftMax + 1
}

116. 填充每个节点的下一个右侧节点指针

image-20220915231157978

解题思路：

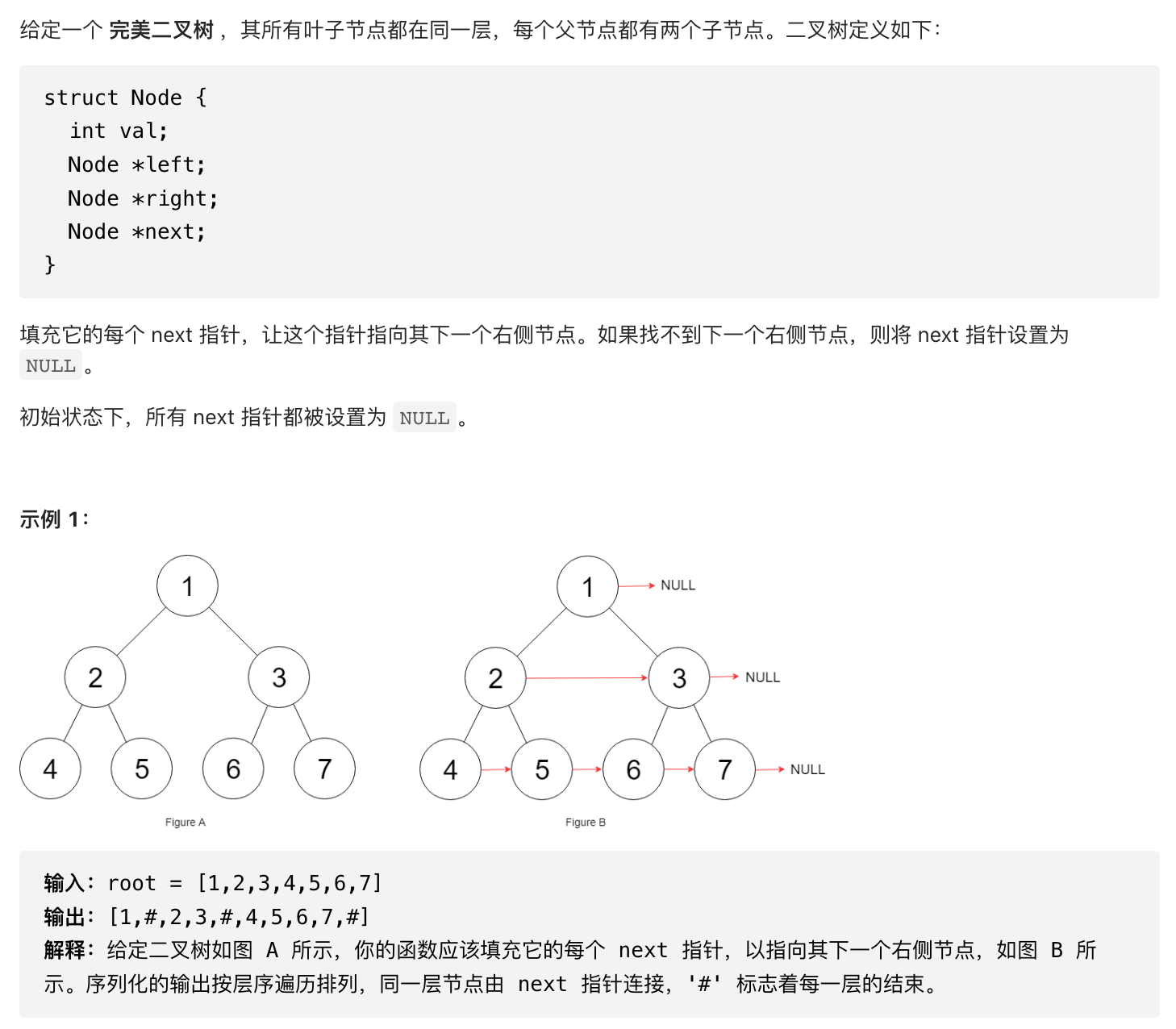
此题中二叉树的左右节点连接很简单，比如示例中的2 -> 3，4 -> 5，6 -> 7，比较难得是左右节点子节点之间的连接，比如5 -> 6的连接，采用分解问题的思路：

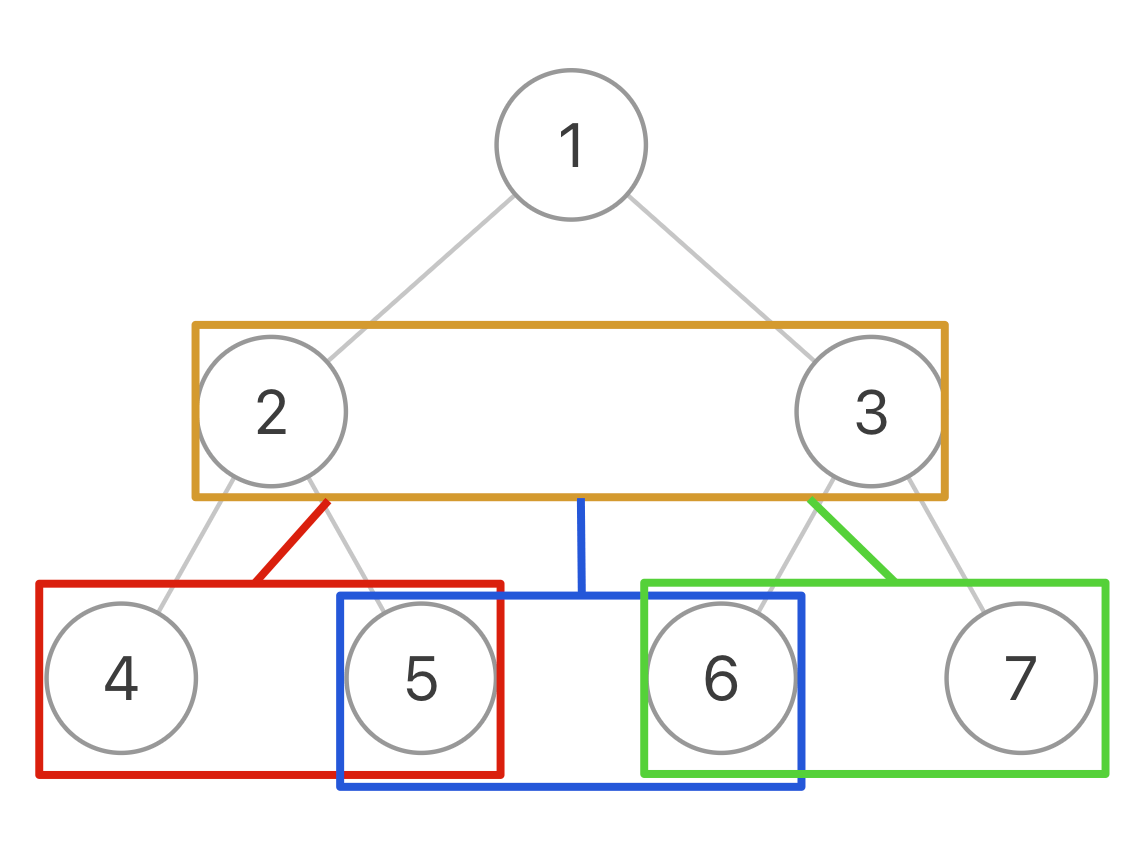
我们把两个二叉树中两个节点抽象成一个节点，这样一颗二叉树就变成了「三叉树」，然后我们遍历这颗「三叉树」，把每个「三叉树节点」中的连个节点链接就可以了，下图中的每个方块看做是一个节点

img

示例代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
func connect(root *Node) *Node {
   	connectTraverse(root.Left, root.Right)
   	return root
}

// 三叉树遍历
func connectTraverse(leftNode *Node, rightNode *Node) {
   	if leftNode == nil || rightNode == nil {
      	return
   	}
   	// 首先连接自身
   	leftNode.Next = rightNode

   	// 连接相同父节点的两个子节点
   	connectTraverse(leftNode.Left, leftNode.Right)
   	connectTraverse(rightNode.Left, rightNode.Right)
   	// 连接相邻节点的子节点
   	connectTraverse(leftNode.Right, rightNode.Left)
}

思考：上述函数还有优化空间吗？

有，在连接相同父节点的两个子节点时，左子树的右节点，和右子树的左节点已经完成了其子节点的连接，在连接相邻节点的时候会重复，即leftNode.Right.Left -> leftNode.Right.Right和rightNode.Left.Left -> rightNode.Left.Right，可以小优化一下，但不优化也问题不大

226. 翻转二叉树

image-20220915234910970

解题思路：

遍历每一个节点，交换每个节点的子节点

示例代码：

1
2
3
4
5
6
7
8
9
func invertTree(root *TreeNode) *TreeNode {
    if root == nil {
		return root
	}
	root.Left, root.Right = root.Right, root.Left
	invertTree1(root.Left)
	invertTree1(root.Right)
	return root
}

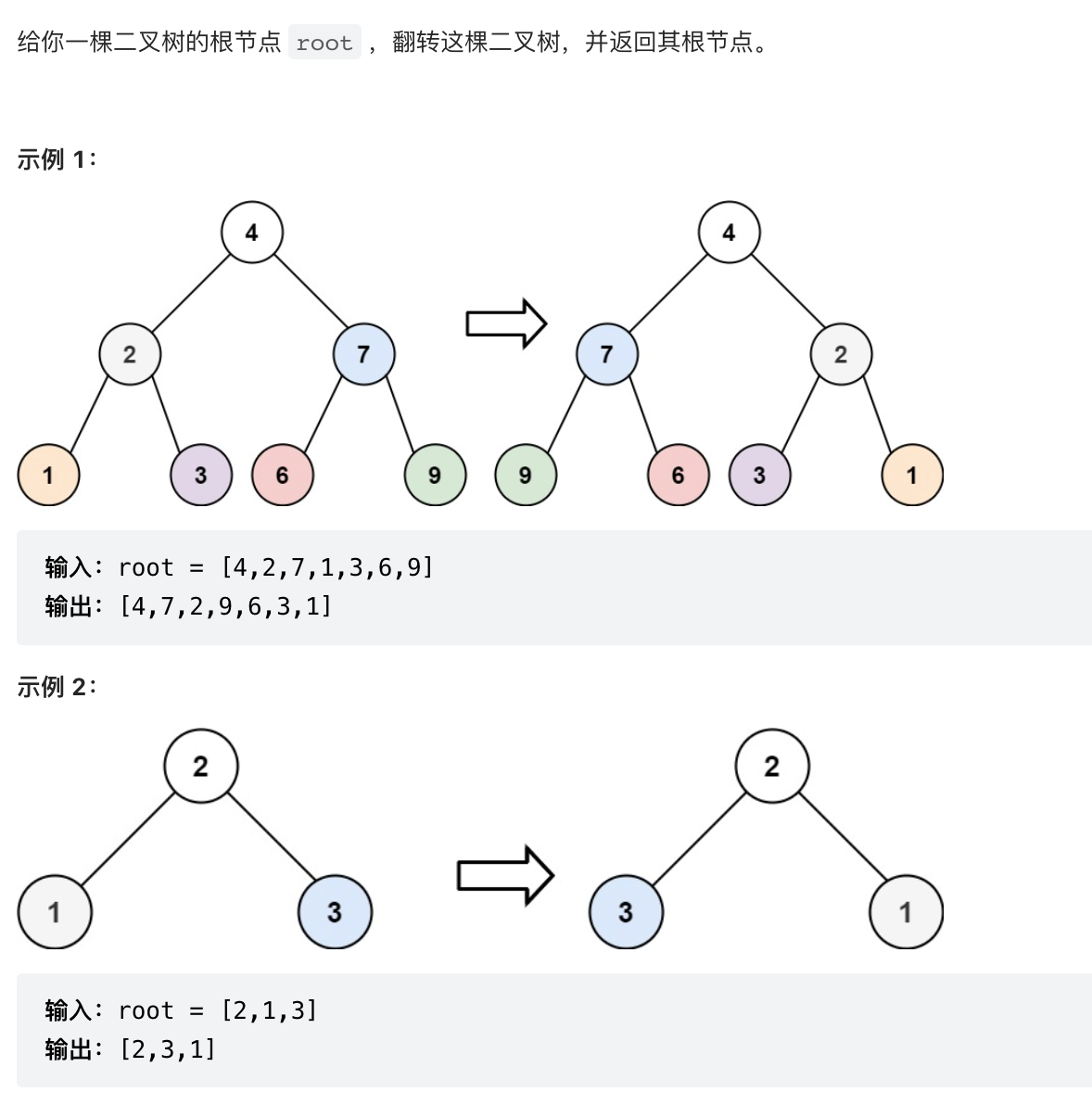
解题思路：

将树分解成N个树，每棵树先翻转自己的左右子树，然后交换左右子节点，放回翻转完的树，将他们组合起来就可以了。

示例代码：

1
2
3
4
5
6
7
8
9
10
11
func invertTree(root *TreeNode) *TreeNode {
	if root == nil {
		return root
	}
	left := invertTree(root.Left)
	right := invertTree(root.Right)

	root.Left = right
	root.Right = left
	return root
}

543. 二叉树的直径

image-20220916001541457

解题思路：

此题关键在于每一条二叉树的「直径」，就是一个节点的左右子树的最大深度之和

使用分解的思路，分别计算出每个节点的左右最大深度，相加之后加上自身返回给上级，组合起来就求出了每个节点的最大直径，取其中最大的一个即可

示例代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
var maxDiameter int

func diameterOfBinaryTree(root *TreeNode) int {
	return diameter(root)
}

func diameter(node *TreeNode) int {
	if node == nil {
		return 0
	}
	//
	leftDiameter := diameter(node.Left)
	rightDiameter := diameter(node.Right)

	diameter := leftDiameter + rightDiameter
	maxDiameter = max(maxDiameter, diameter)

	if leftDiameter > rightDiameter {
		return leftDiameter + 1
	}
	return max(leftDiameter, rightDiameter) + 1
}

func max(a, b int) int {
	if a > b {
		return a
	}
	return b
}

参考链接：